Angulos determinado por Rectas Paralelas cortadas po una Secante
Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:
Las recta r corta a las rectas paralelas m y n:
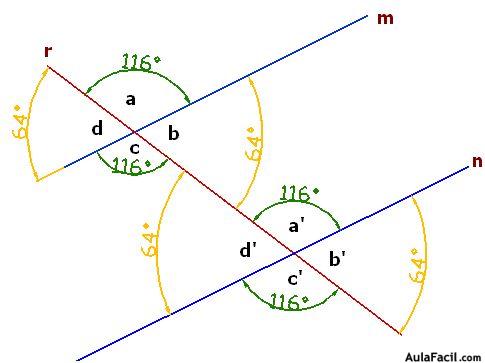
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:
Interiores o internos:
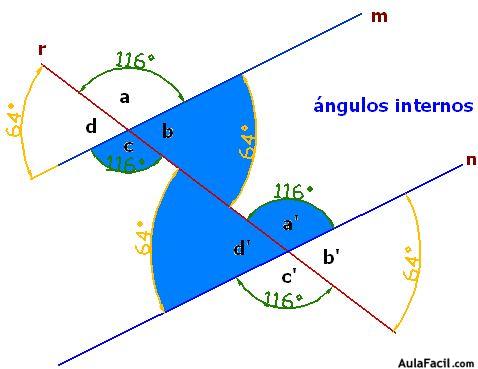
En azul, son los que se encuentran entre las rectas paralelas.
Ángulos exteriores o externos:
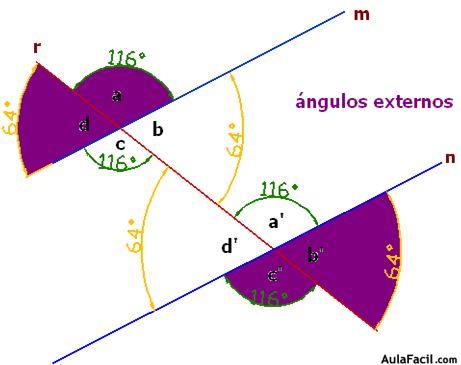
Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.
Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
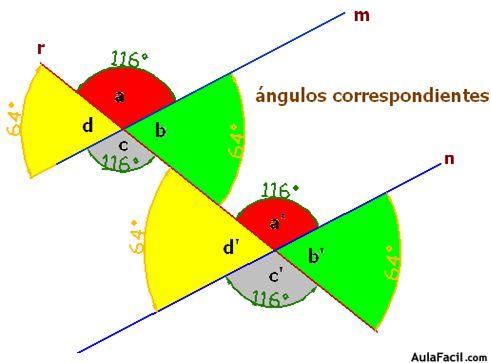
Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.
Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:
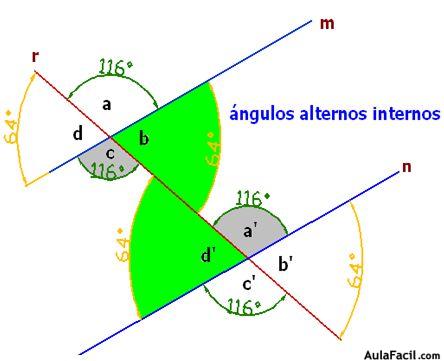
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.
Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:
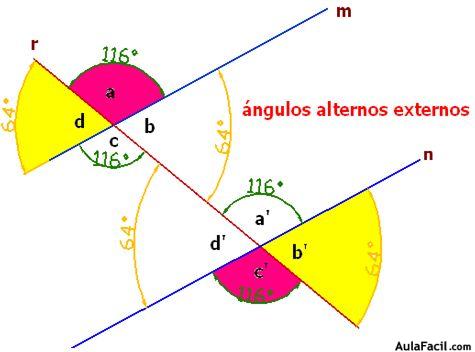
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.
15.55 Observa la figura siguiente y después, contesta a las preguntas siguientes:
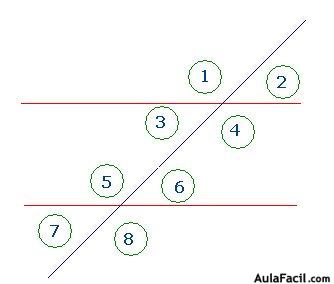
- ¿Cómo son los ángulos 1 y 2?
- ¿Cómo podemos llamar a los ángulos 1 y 4?
- ¿Son suplementarios los ángulos 2 y 4?
- ¿Son iguales los ángulos 2 y 3? ¿Por qué?
- ¿Son correspondientes los ángulos 3 y 7?
- ¿Cómo son los ángulos 4 y 6?
- ¿Es el ángulo 6 correspondiente al ángulo 3?
- ¿Son iguales los ángulos 5 y 8? ¿Por qué?
- ¿Cómo puedes llamarles a los ángulos 1 y 8?
- ¿Son alternos internos los ángulos 5 y 6?
Respuestas:
- Adyacentes y suplementarios.
- Opuestos por el vértice. Uno es externo y el otro interno.
- Sí, juntos valen 180º.
- Sí, por ser opuestos por el vértice.
- Sí por encontrarse en el mismo lado de la secante, siendo uno un ángulo interior y el otro un ángulo exterior.
- Se encuentren en el mismo lado de la secante, los dos son ángulos interiores.
- No porque no están situados al mismo lado de la secante y además, los dos son interiores.
- Sí por estar opuestos por el vértice.
- Son ángulos alternos externos ya que se encuentran a distinto lado de la secante y en la parte exterior de las paralelas.
- No porque no son alternos y además, los alternos internos son iguales entre sí.